07. 线性变换
线性节点的解决方案
下面是上一道练习我的解决方案:
class Linear(Node):
def __init__(self, inputs, weights, bias):
Node.__init__(self, [inputs, weights, bias])
def forward(self):
"""
Set self.value to the value of the linear function output.
Your code goes here!
"""
inputs = self.inbound_nodes[0].value
weights = self.inbound_nodes[1].value
bias = self.inbound_nodes[2]
self.value = bias.value
for x, w in zip(inputs, weights):
self.value += x * w在该解决方案中,我将 self.value 设为偏置,然后循环访问输入和权重,将每个加权输入加到 self.value 上。注意,对 self.inbound_nodes[0] 或 self.inbound_nodes[1] 调用 .value 会得出一个列表。
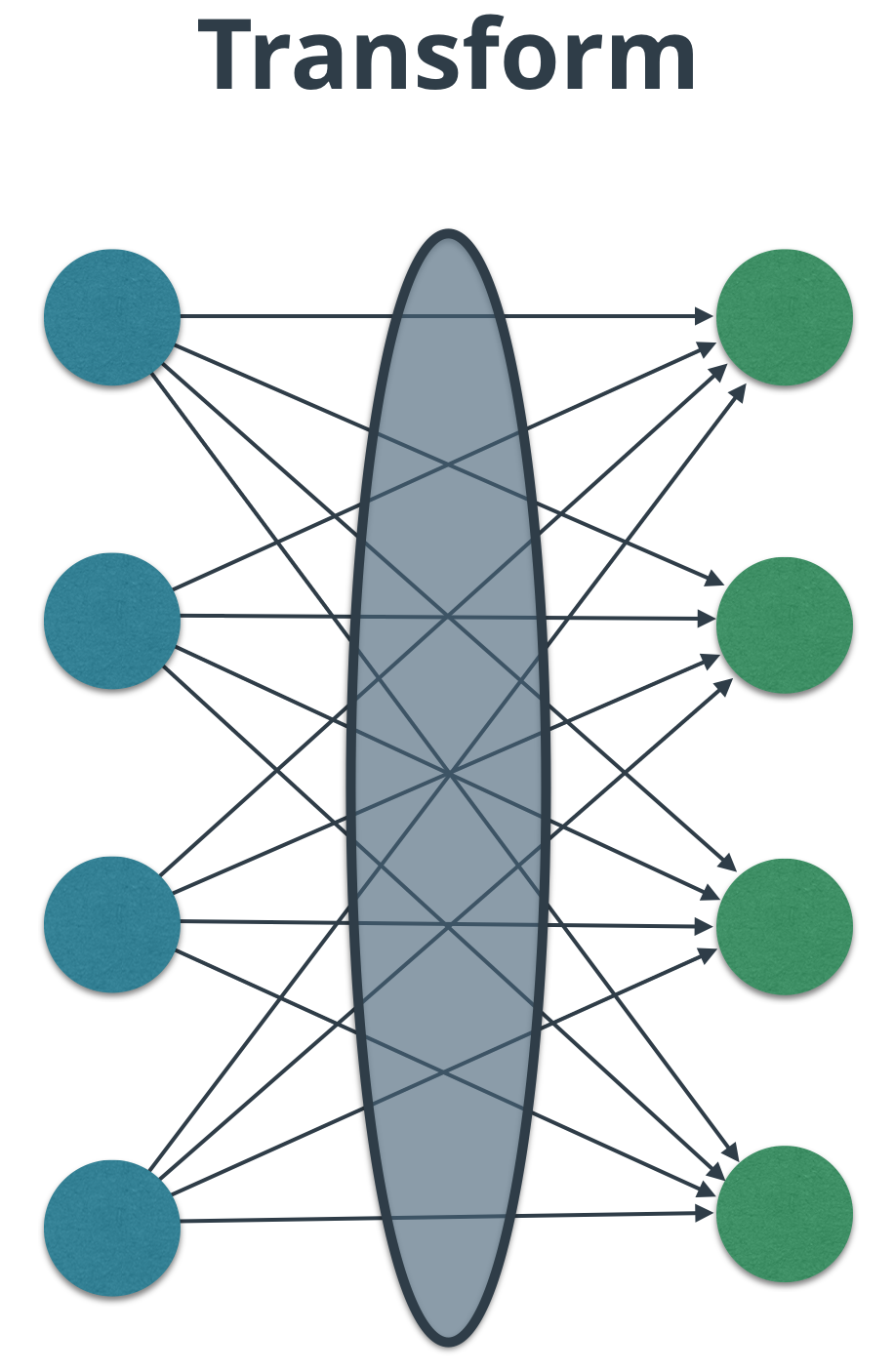
注意多个层之间的边。
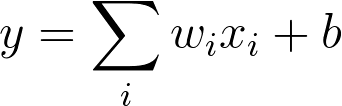
Equation (1)
对于这节课的后续部分,我们将 x 表示为 X,将 w 表示为 W,因为现在它们是矩阵了,b 现在是向量,而不是标量了。
假设有个 Linear 节点,具有 1 个输入和 k 个输出(将 1 个输入映射到 k 个输出)。在此背景下,输入/输出就等同于特征。
在这种情况下,X 是 1 x 1 的矩阵。
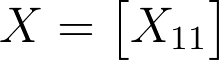
1 by 1 matrix, 1 element.
W 变成 1 x k 的矩阵(看起来像一行)。
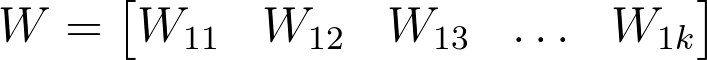
1 x k 权重行矩阵。
X 和 W 的矩阵相乘结果是 1 x k 的矩阵。因为 b 也是 1 x k 的行矩阵(1 个偏置/输出),b 加到 X 和 W 矩阵相乘的输出上。
如果我们将 n 个输入映射到 k 个输出上呢?
那么 X 变成 1 x n 的矩阵,W 变成 n x k 的矩阵。矩阵相乘的结果依然是 1 x k 矩阵,所以偏置的使用保持不变。
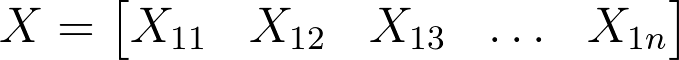
X 现在是 1 x n 的矩阵,n 个输入/特征。
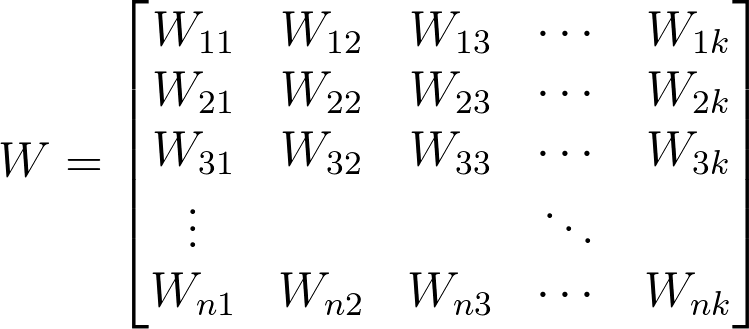
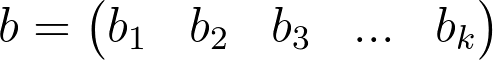
偏置的行矩阵,每个输出一个。
我们来看看具有 n 个输入的示例。假设有个 28px x 28px 的灰度图片,和 MNIST 数据集中的图片一样,是一组手写的数字。我们可以调整图片的形状,使其变成 1 x 784 的矩阵,n = 784。每个像素是一个输入/特征。下面是一个动画示例,强调像素是一种特征。
像素是特征!
实际操作中,我们通常会向每个向前传递提供多个数据示例,而不是只有 1 个。这么做的原因是示例可以平行处理,大大提高了性能。示例数量称为批量大小。批量大小的常见数字包括 32、64、128、256、512。通常是我们可以正好放入内存中的数字。
对 X、W 和 b 来说意味着什么?
X 变成 m x n 的矩阵,W 和 b 保持不变。矩阵相乘的结果现在变成 m x k, 所以加上 b 变成每行的广播。
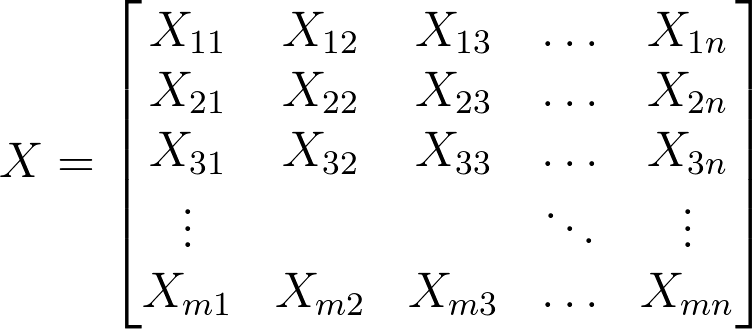
X 现在是 m x n 的矩阵。每行有 n 个输入/特征。
对于 MNIST 来说,X 的每行是从 28 x 28 变成 1 x 784 的图片。
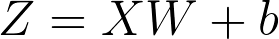
等式 (2)
等式 (2) 还可以看做 Z = XW + B,其中 B 是偏置向量 b 当做行堆叠 m 次。由于广播原因,缩写为 Z = XW + b。
请重新构建 Linear 以使用 Python 匹配程序包 numpy 处理矩阵和向量,使你操作起来更轻松。numpy 经常缩写为 np,所以当我们在代码中提到时,将写成 np。
我使用 np.array (文档) 创建了矩阵和向量。你需要使用 np.dot,它充当的是二维数组的矩阵乘法 (文档),将等式 (2) 的输入和权重矩阵相乘。同时注意,numpy 实际上过载了 __add__ 运算符,使你能够直接在 np.array(例如 np.array() + np.array())中使用。
说明
- 打开 nn.py。看看神经网络如何实现了
Linear代码。 - 打开 miniflow.py。在
Linear代码的前向传递中实现等式 (2)。 - 测试你的代码!
Start Quiz: